Photoconductivité dépendante du spin dans les matériaux 2D
La résonance électronique de spin (ESR) est une technique spectroscopique qui utilise une onde électromagnétique pour sonder les électrons non appariés, qu’ils proviennent de défauts ponctuels, de centres paramagnétiques ou des électrons de conduction. Les spectromètres commerciaux fonctionnent en général dans la bande X (8–12 GHz), avec des champs magnétiques inférieurs au tesla. À plus haute fréquence, la spectroscopie de photoconductivité GHz–THz développée au sein de l’équipe permet de détecter des résonances de spin qui modifient directement la conductivité par des processus de recombinaison dépendants du spin.
Ces recherches visent à utiliser cette technique pour explorer les gaps topologiques, les effets de proximité spin–orbite, les motifs de Moiré, ainsi que la dynamique de spin dans les hétérostructures de matériaux 2D, pour mieux comprendre les interactions fondamentales du spin dans la matière condensée.
Dans le graphène, cette approche a récemment permis de mesurer un gap de Kane–Mele d’environ 45 µeV [Phys. Rev. B 106, 245141 (2022)]. Ce gap, ainsi que les splittings à champ nul, peuvent être modulés par effet de proximité avec d’autres matériaux bidimensionnels, en jouant sur le champ électrique, le couplage spin–orbite ou les effets de Moiré. La dimensionnalité influe également sur les temps de relaxation de spin, particulièrement longs dans le graphène du fait de son faible couplage spin–orbite. Enfin, l’effet de saturation ESR permet de sonder les mécanismes de relaxation spin–spin et spin–réseau [Phys. Rev. Appl. 23, 044043 (2025)].
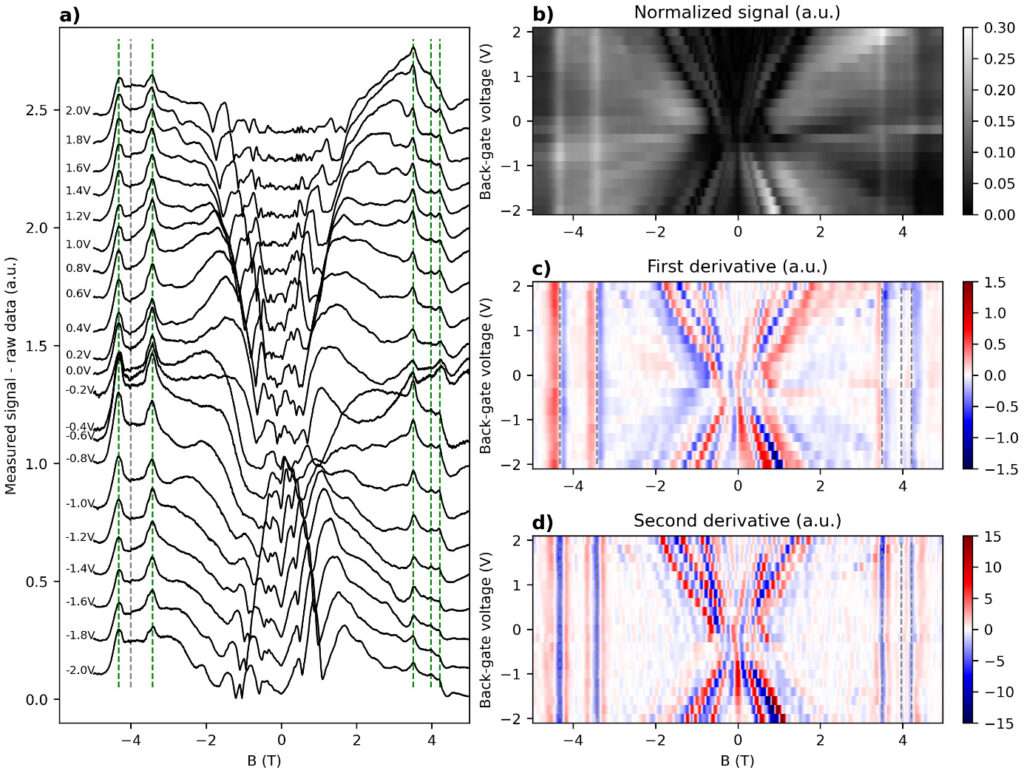
Signal de photoconductivité mesuré en fonction du champ magnétique, pour différentes tensions de grille arrière. La caractéristique en forme de X à faible champ indique la présence d’oscillations de type Shubnikov-de Haas. À des champs magnétiques plus élevés, plusieurs transitions apparaissent nettement sous forme de lignes verticales. La valeur absolue du signal normalisé est représentée sous forme de carte de couleurs b), avec la dérivée première et seconde en c) et d). Crédit : Phys. Rev. B 106, 245141 (2022)